Abstract

Sketch-and-extrude is a common and intuitive modeling process in computer aided design. This paper studies the problem of learning the shape given in the form of point clouds by inverse sketch-and-extrude. We present ExtrudeNet, an unsupervised end-to-end network for discovering sketch and extrude from point clouds. Behind ExtrudeNet are two new technical components: 1) an effective representation for sketch and extrude, which can model extrusion with freeform sketches and conventional cylinder and box primitives as well; and 2) a numerical method for computing the signed distance field which is used in the network learning. This is the first attempt that uses machine learning to reverse engineer the sketch-and-extrude modeling process of a shape in an unsupervised fashion. ExtrudeNet not only outputs a compact, editable and interpretable representation of the shape that can be seamlessly integrated into modern CAD software, but also aligns with the standard CAD modeling process facilitating various editing applications, which distinguishes our work from existing shape parsing research.

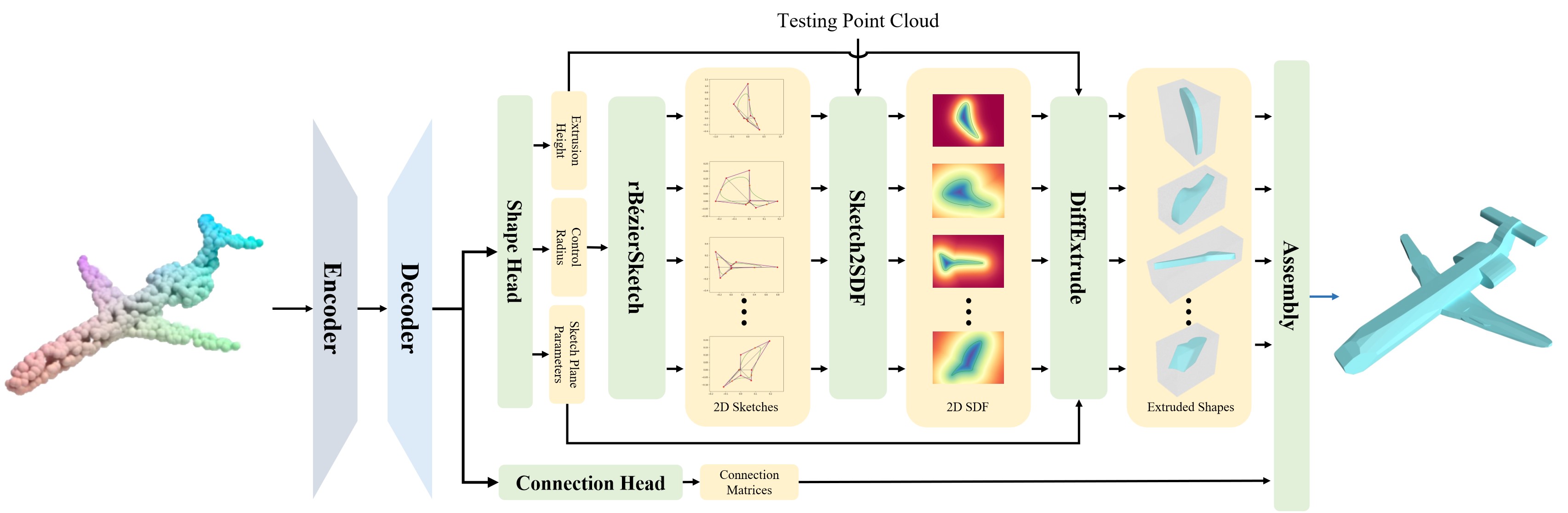
ExtrudeNet Structure

We take inspiration from the process of sketch and extrude, a popular and intuitive approach widely used in the field of computer aided design (CAD) where engineers usually model shapes by first sketching a closed free form sketch (profile) in a 2D sketch plane and then extruding the sketch into 3D. To realize ExtrudeNet, we create three modular components: 1) rBezierSketch , which generates a simple closed curve (i.e.\ no self-intersection); 2) Sketch2SDF , a versatile numerical method for computing Signed-Distance-Field from parametric curves; and 3) , a differentiable method for extruding 2D Signed-Distance-Field (SDF) into a 3D solid shape. Built upon these components, ExtrudeNet takes a point cloud as input and outputs sketch and extrude parameters which form a compact, interpretable and editable shape representation.

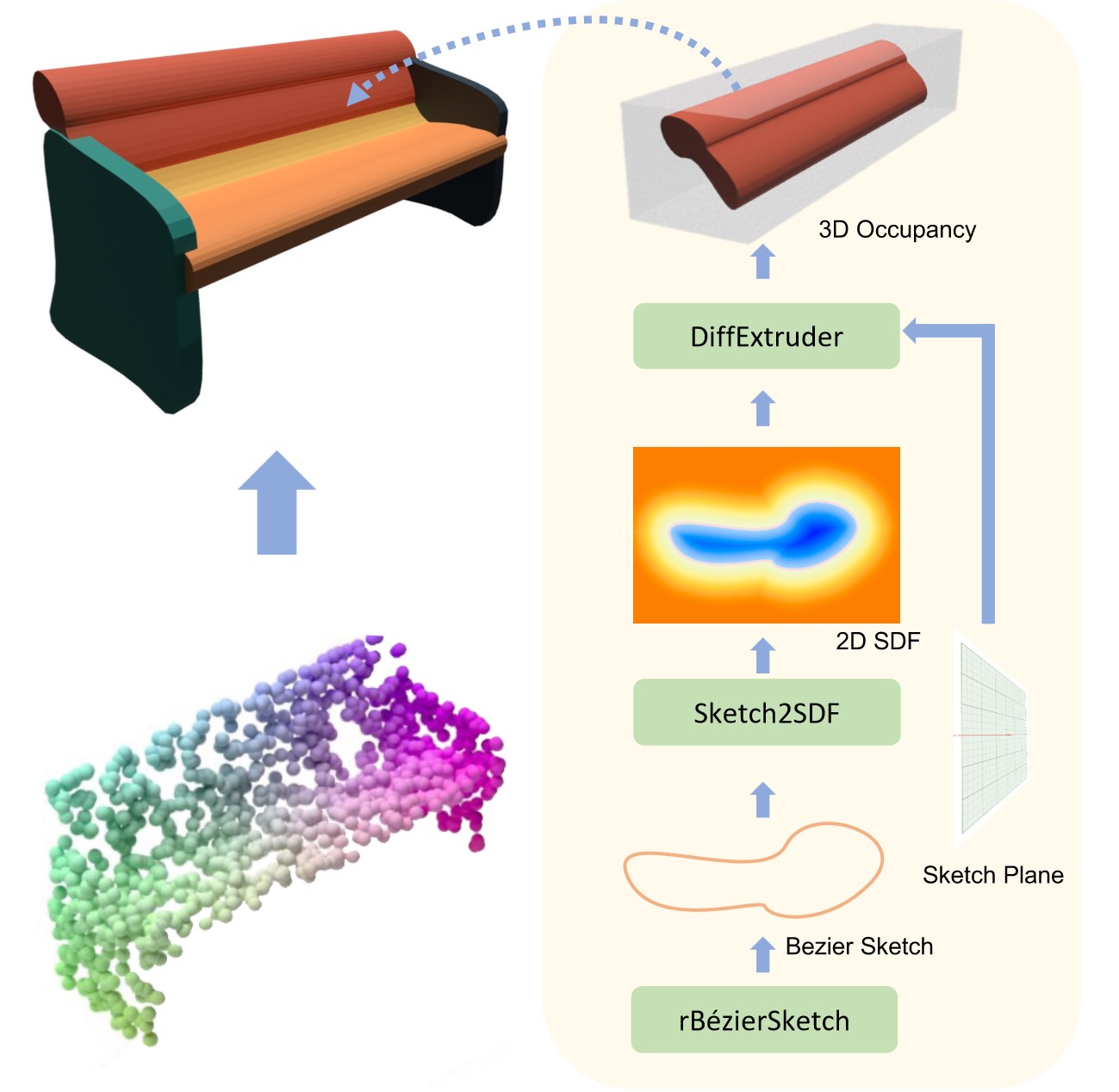
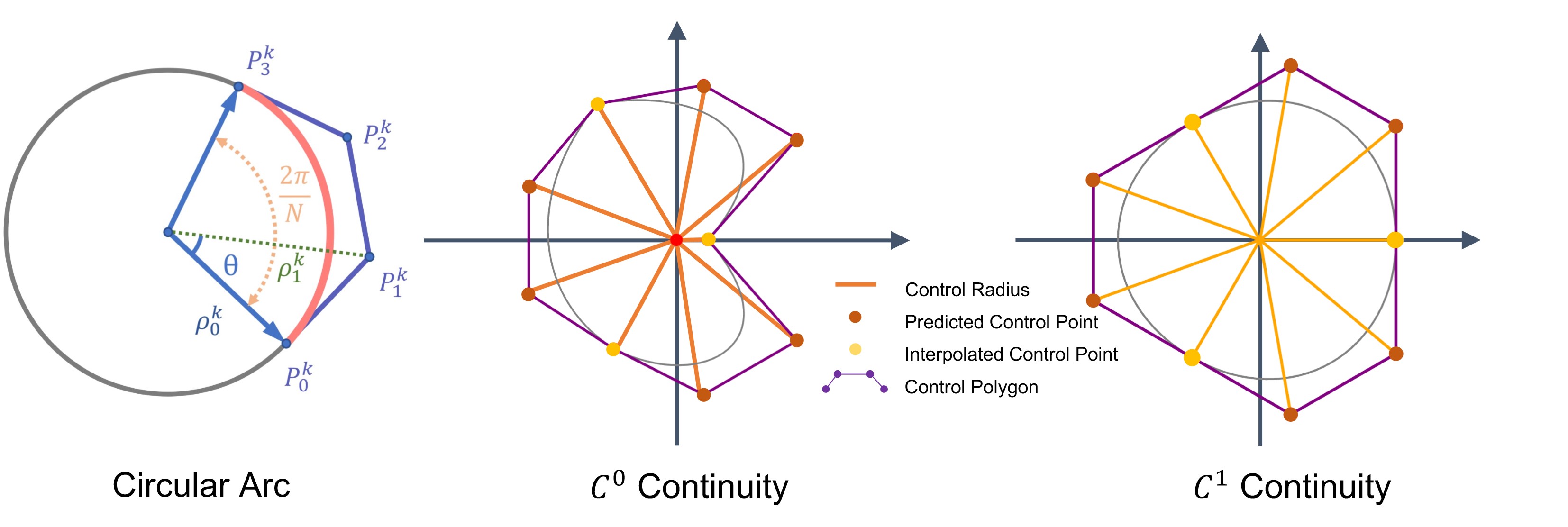
rBezierSketch

rBezierSketch is designed with the following benifits in mind.

Compatible with industry standards as it is a simple form of NURBS
It can represent straight lines, circles and free-form curves in a uniform representation
It represent a star-convex set and will not self intersect
It can be constraint to generate only C1 continuous sketch

The basic mathematical model is a closed curve formed by N curve segments defined by special rational cubic Bezier curves $$ C_k(t), t\in [0,1], k=0,1,\cdots,N-1 $$ The equation for each curve segment is: $$ C_k(t) = \frac{P^k_0B_0^3(t)+ w^k_1 P^k_1B_1^3(t)+ w^k_2 P^k_2B_2^3(t)+ P^k_3B_3^3(t)}{B_0^3(t)+w^k_1 B_1^3(t)+ w^k_2B_2^3(t)+B_3^3(t)} $$ We use the polar coordinate system to help define the control points P, where: $$ P^k_i = (x^k_i, y^k_i) = (\rho_i^k\cos(\alpha_i^k), \rho^k_i\sin(\alpha^k_i)) $$ $$ \alpha^k_1= \alpha^k_0+\theta,\;\; \alpha^k_3 = \alpha^k_0+\frac{2\pi}{N},\;\; \alpha^k_2 = \alpha^k_3-\theta $$ $$ \displaystyle \theta =\frac{2\pi}{4N}+\tan^{-1}\left(\frac{1}{3}\tan\left(\frac{2\pi}{4N}\right)\right) $$ These angles are specially designed to achieve the above stating benifits. (see paper for details)

Sketch2SDF

We present a numerical method for computing the SDF of simple parametric sketches. The method is general. While it applies to the rational cubic Bézier curves here, it also works for other parametric curves. This method also yields good gradients which is friendly for deep learning applications. The SDF of a sketch is defined by the Distance-Field DF(p), the smallest distance from a given testing point p to the curve, multiplied by a sign SIGN(p) which indicates whether the testing point p is inside or outside of the sketch. We first sample a set of sample points from the curve $$ S =\left\{\left(x(\frac{i}{n}),y(\frac{i}{n})\right)\mid i=0,1,\cdots,n\right\} $$ and the distance field can be approximated by $$ DF(p)= \underset{s\in S}{\min} \|s-p\|_2 $$ the normal of each sample point is computed $$ N(t) = \left(\frac{d y(t)}{dt}, -\frac{d x(t)}{dt}\right) $$ the sign can be computed as follow $$ SIGN(p)= \frac{N(CT(p))\cdot (C(CT(p))-p)}{\|N(CT(p))\cdot (C(CT(p))-p)\|_2 + \epsilon} $$ put them together, the final sdf is equal to $$ SDF_s(p) = SIGN(p) \times DF(p). $$

Extrusion

We first transform the testing point p back to a point p' by reversing the transformations that transform the XY-plane to the target sketch plane. Then we compute the signed distance of p' with respect to the upright extrusion shape whose base lies on the XY-plane If the testing point is inside the extruded shape $$ SDF_i(p') = \max(\min(SDF_s((p'_x, p'_y)), h-p'_z, p'_z), 0) $$ otherwise $$ SDF_o(p') = -[ (\min(h-p'_z,0))^2+(\min(p'_z,0))^2 \mbox{} +(\min(SDF_s((p'_x, p'_y)),0))^2 ]^{\frac{1}{2}} $$ Finally, the overall SDF is the sum of the two cases. $$ SDF(p') = SDF_i(p') + SDF_o(p') $$

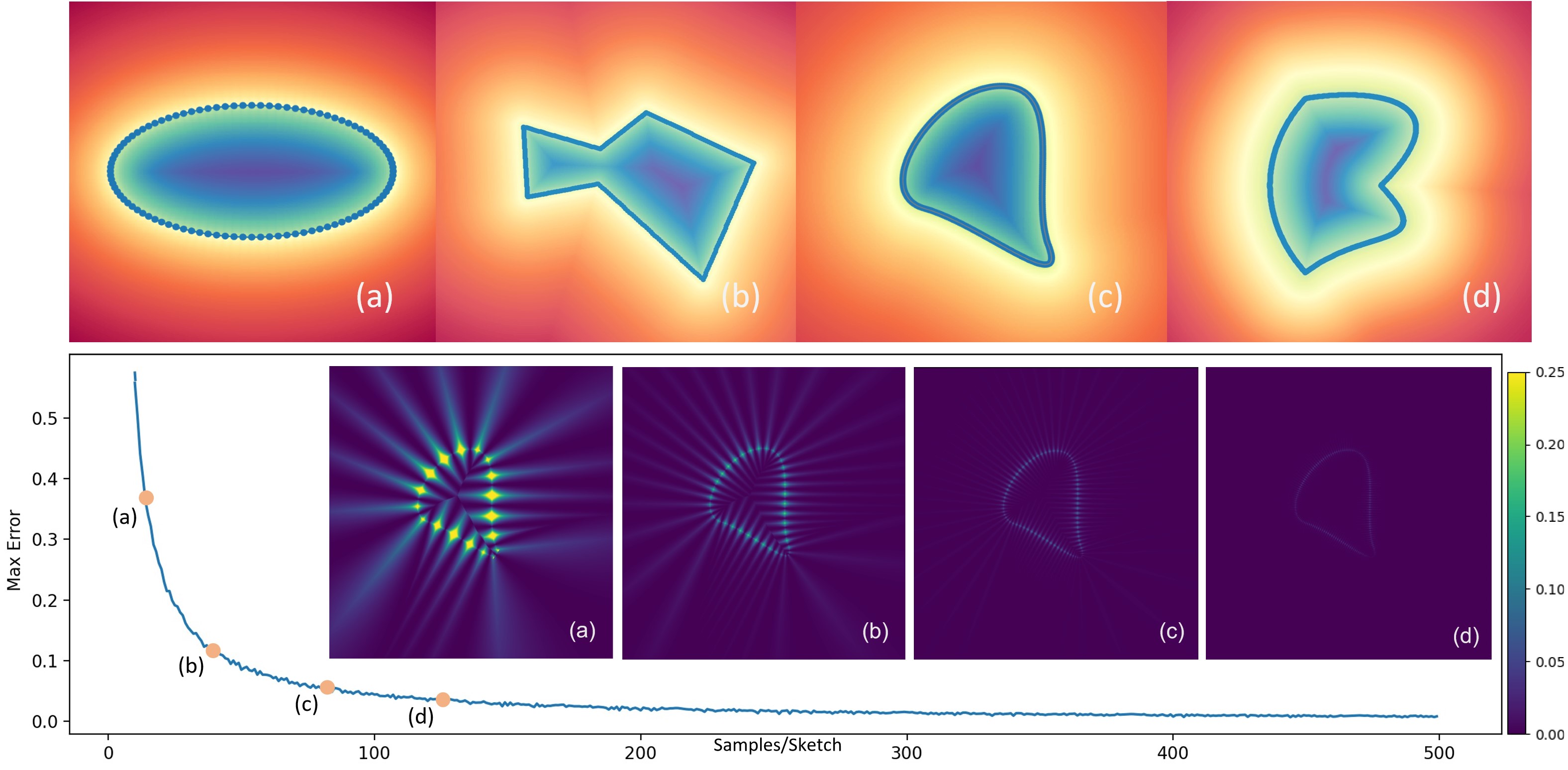
Evaluation of rBezierSketch

Approximability

To demonstrate the approximation ability and the ease of learning of the proposed rBezierSketch, we conduct a fitting experiment that directly optimize for the radial coordinate that best reconstructs a given raster emoji image.

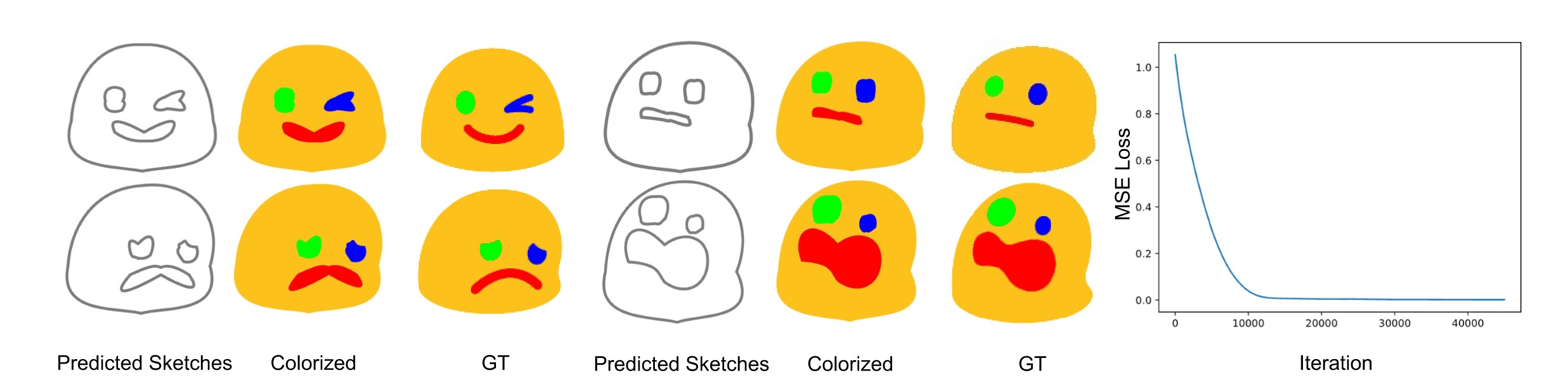
Versatility and error analysis

To show the versatility, we implemented four different kinds of parametric curves, namely polygon, ellipse, Cubic Bezier Sketchs with C1 and C0 continuity. Note that our method is not limited to these curves, and can be easily adapted to new parametric curve types. We also plot the error introduced by apprimation by comparing our results with analytical results.

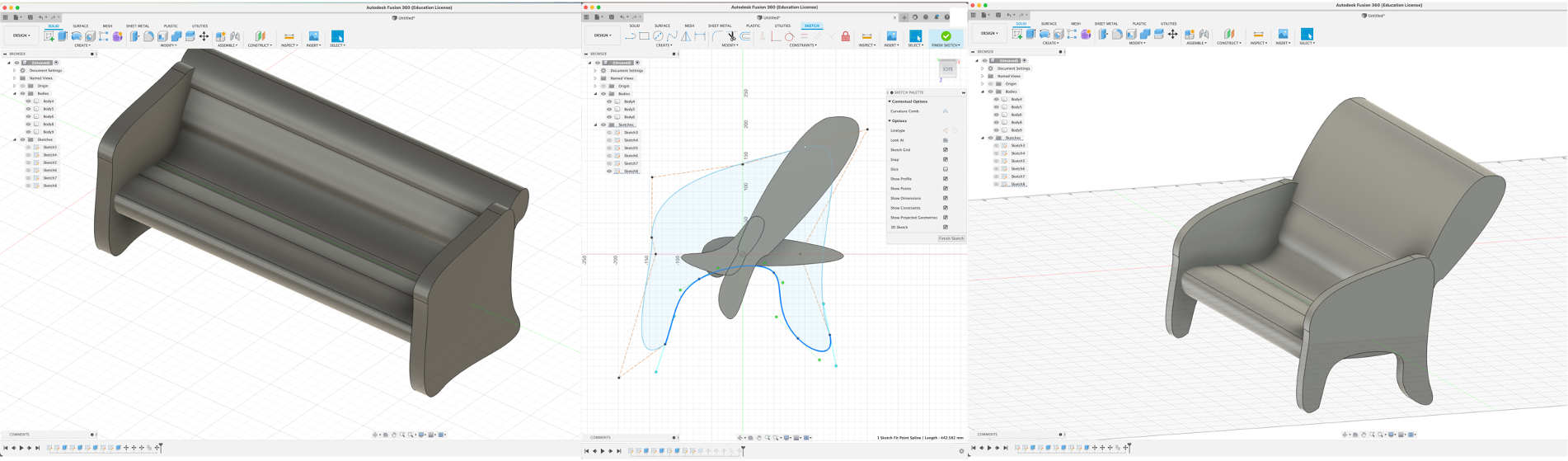
Edibility of Sketch and Extrude

As rBezier sketch is essentially a cubic rational bezier curve and Extrusion is a typical operation for B-Rep representation, our results are well compatiable to popular CAD software.

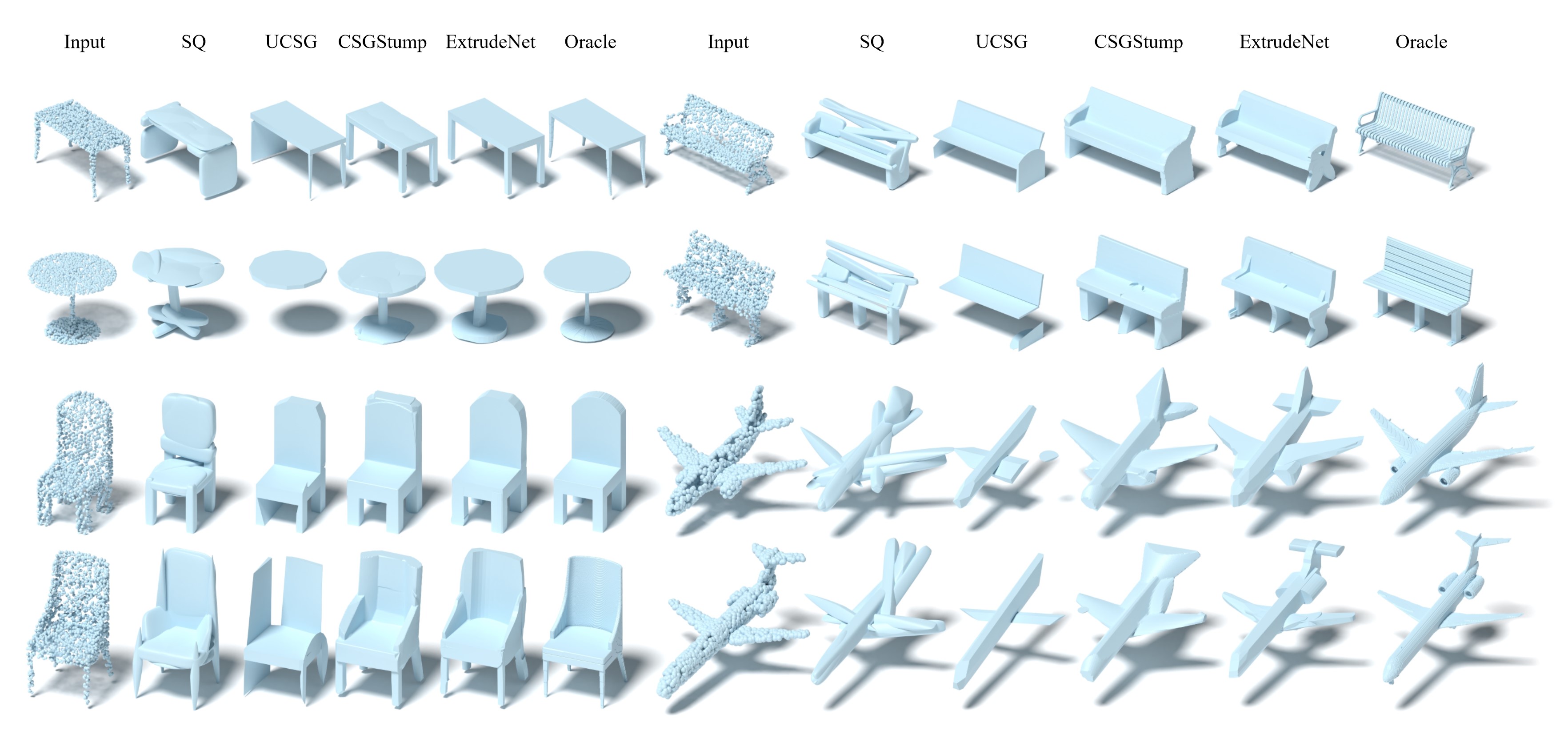
Comparison on Geometric Evaluation Results

The following figure shows the qualitative comparison with baselines, We can see our method achieves better geometry approximation with fewer primitives.

Acknowledgement

The work is partially supported by a joint WASP/NTU project (04INS000440C130), Monash FIT Startup Grant, and SenseTime Gift Fund.