CSG-Stump: A Learning Friendly CSG-Like Representation for Interpretable Shape Parsing

 |
 |
Abstract
Generating an interpretable and compact representation of 3D shapes from point clouds is an important and challenging problem. This paper presents CSG-Stump Net, an unsupervised end-to-end network for learning shapes from point clouds and discovering the underlying constituent modeling primitives and operations as well. At the core is a three-level structure called CSG-Stump, consisting of a complement layer at the bottom, an intersection layer in the middle, and a union layer at the top. CSG-Stump is proven to be equivalent to CSG in terms of representation, therefore inheriting the interpretable, compact and editable nature of CSG while freeing from CSG's complex tree structures. Particularly, the CSG-Stump has a simple and regular structure, allowing neural networks to give outputs of a constant dimensionality, which makes itself deep-learning friendly. Due to these characteristics of CSG-Stump, CSG-Stump Net achieves superior results compared to previous CSG-based methods and generates much more appealing shapes, as confirmed by extensive experiments.
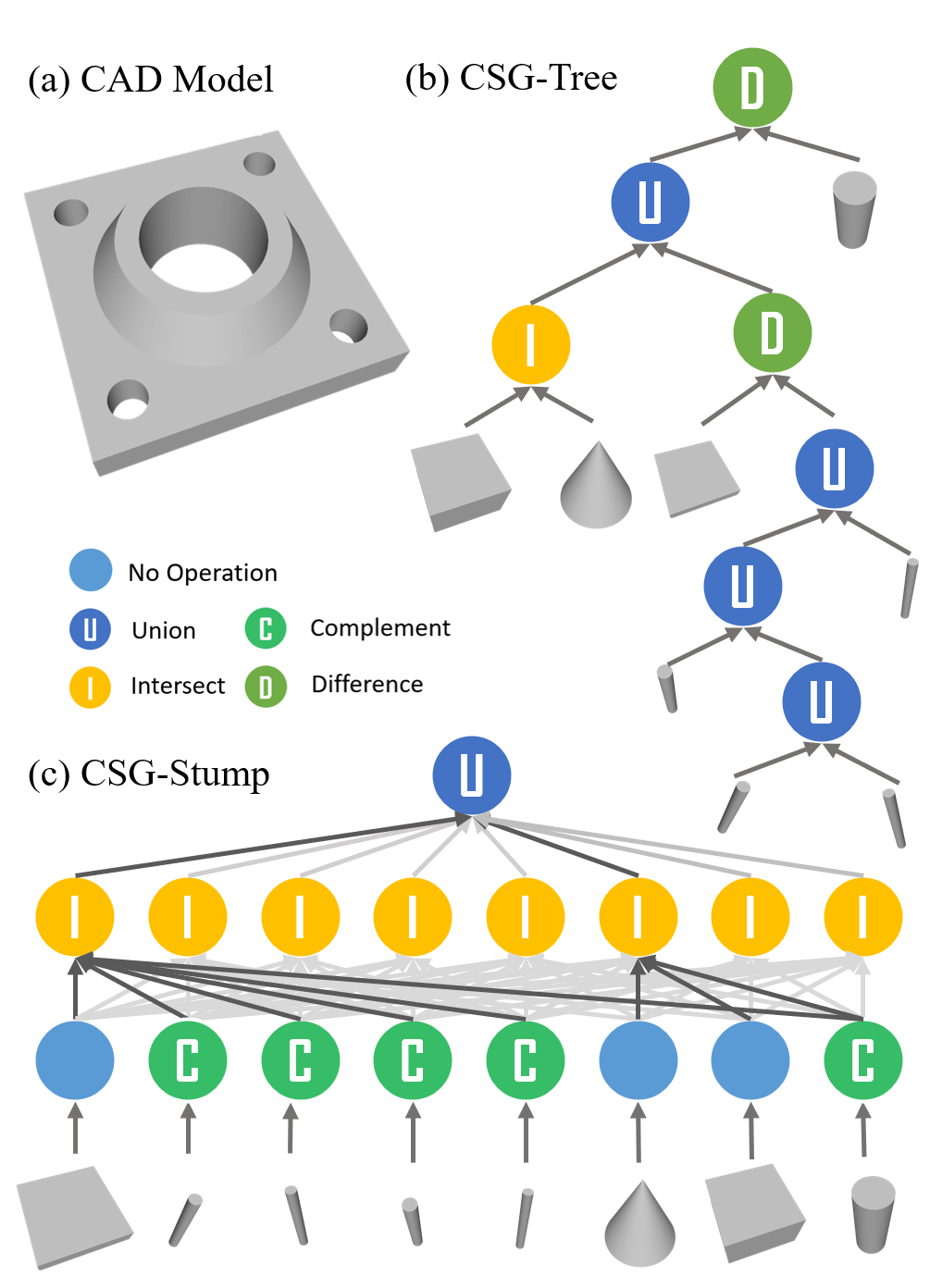
CSG-Stump Structure
In this paper, we propose CSG-Stump, a novel and systematic reformulation of CSG-Tree, a hierarchical 3D shapes representation with nodes storing operation information, but with fixed three layers. A complement layer is at the bottom, at which nodes store whether the complement operation is performed on their corresponding one-to-one primitives. An intersection layer is in the middle, at which nodes record which shapes generated in the bottom layer are selected for the intersection operation. A union layer with only one node is at the top, recording which shapes generated in the intersection layer are selected for the union operation.
We denote the whole space and the empty set by U and ∅ respectively. Therefore, the complement of a shape is implemented by the difference of the shape with U. Intersecting an object with U gives the object itself and the union of an object and ∅ returns the object itself. Specifically, we define a 1 × K matrix WC ∈ {0, 1}K for the complement layer, where K is the number of the primitives; a K × C matrix WI ∈ {0, 1}K ×C for the intersection layer, where C(≤ K) is the number of nodes in the intersection layer; and a C × 1 matrix WU ∈ {0, 1}C for the union layer.
Each entry in these matrices takes a value of either 1 or 0. In particular, WC [1, i] = 0 or 1 encodes whether the shape of primitive i or its complement is used for node i of the complement layer. If WI [j, i] = 1, the shape from node j in the complement layer is selected for the intersection in node i of the intersection layer, and similarly, WU [j, 1] implies that the shape from node j in the intersection layer is selected for the union operation at the top layer. In this way, CSG-Stump represents a shape by a set of primitive shapes and three connection matrices.
To facilitate shape analysis and problem formulation, we describe the nodes of CSG-Stump by mathematics functions. First, we define a shape O by an occupancy function O(x) : R3 → {0, 1} as follows:
\begin{equation} O(x) = \left\{ \begin{array}{ll} 1, & x \;\;\text{is within the shape}\\ 0, & \text{otherwise} \end{array} \right. \end{equation}
Thus U(x) ≡ 1 and ∅(x) ≡ 0. The complement of primitive object Oi can be defined by function: $$O_i^c(x)= 1-O_i(x)$$ the intersection of k objects: $$\min_{i = 1 \dots k}(O_i(x))$$ the union of k objects: $$ \max_{i = 1 \dots k}(O_i(x))$$ the difference of two objects: $$\min\left(O_i(x), 1-O_j(x)\right)$$
With the binary connection matrices WC , WI and WU , each node in the CSG-Stump structure can be defined by a certain function.
For each node i = 1,···,K in the first layer, its shape Fi can be defined by function Fi(x):
\begin{equation}\label{eq:Fi} F_i(x) = W_C[1,i]\times (1-O_i(x)) + (1-W_C[1,i])O_i(x). \end{equation}
For each node i = 1,···,C in the second layer, its shape Si is an intersection of nodes from the first layer, and can thus be defined by function Si(x):
\begin{equation} \label{eq:Si} S_i(x) = \min_{1 \le j\le K}(W_{I}[j,i] \times F_j(x) + (1-W_{I}[j,i]) \times 1). \end{equation}
For the node in the third layer, its shape T is the union of nodes from the second layer, and can thus be defined by function T (x):
\begin{equation}\label{eq:Tx} T(x) = \max_{1\le j\le C}(W_{U}[j,1] \times S_j(x) + (1-W_{U}[j,1]) \times 0). \end{equation}
Now for a input shape given by a point cloud X = {xi}N consisting of a list of 3D points xi, we can first obtain the target shape occupancy Oi as aboved occupancy function O(x) and then detect the underlying primitives with a RANSAC-like method. Then reconstructing a CSG-like representation for the shape is simplified to finding the three connection matrices which can be formulated as a Binary Programming problem.
let Ok(i) represents the occupancy value of testing point i for primitive k and T(i) represents the estimated occupancy of point i. The connection matrices WC,WI and WU for the selection process of CSG-Stump are the solution of the following minimization problem:
$$ \small \begin{align} \underset{W_{\{C,I,U\}}}{\text{min.}}& \quad \frac{1}{N}\sum_i^N{\|T(i)-O_i\|}\nonumber\\ \textrm{s.t.}\quad &T(i)=\max_j\{S_j(i) \times W_{U}[j,1] \} \nonumber\\ &S_j(i)=\min_k\{F_{k}(i) \times W_{I}[k,j]+(1-W_I[k,j])\} \nonumber\\ &F_k(i)=(1-O_{k}(i)) W_{C}[1,k] + {O}_{k}(i) (1-W_{C}[1,k]) \nonumber\\ &W_{I}, W_{U}, W_{C}\in\{0,1\},\;\; {O}_{k}(i)\in\{0,1\} \end{align} \normalsize $$
We prove that CSG-Stump is equivalent to typical CSG-Tree in terms of representation, i.e., we can represent anycomplex CSG shape by our three-layer CSG-Stump. Therefore, CSG-Stump inherits the ideal characteristics of CSG-Tree, allowing highly compact, interpretable and editable shape representation while freeing from the limitations of a tree structure. Moreover, CSG-Stump gives rise to two additional advantages: 1) High representation capability. The maximum representation capability can be realistically achieved with CSG-Stump, as opposed to a conventional CSG-Tree that needs many layers for complex shapes. 2) Deep learning-friendly. The consistent structure of CSG-Stump allows neural networks to give fixed dimension output, making network design much easier.
We denote the whole space and the empty set by U and ∅ respectively. Therefore, the complement of a shape is implemented by the difference of the shape with U. Intersecting an object with U gives the object itself and the union of an object and ∅ returns the object itself. Specifically, we define a 1 × K matrix WC ∈ {0, 1}K for the complement layer, where K is the number of the primitives; a K × C matrix WI ∈ {0, 1}K ×C for the intersection layer, where C(≤ K) is the number of nodes in the intersection layer; and a C × 1 matrix WU ∈ {0, 1}C for the union layer.
Each entry in these matrices takes a value of either 1 or 0. In particular, WC [1, i] = 0 or 1 encodes whether the shape of primitive i or its complement is used for node i of the complement layer. If WI [j, i] = 1, the shape from node j in the complement layer is selected for the intersection in node i of the intersection layer, and similarly, WU [j, 1] implies that the shape from node j in the intersection layer is selected for the union operation at the top layer. In this way, CSG-Stump represents a shape by a set of primitive shapes and three connection matrices.
To facilitate shape analysis and problem formulation, we describe the nodes of CSG-Stump by mathematics functions. First, we define a shape O by an occupancy function O(x) : R3 → {0, 1} as follows:
\begin{equation} O(x) = \left\{ \begin{array}{ll} 1, & x \;\;\text{is within the shape}\\ 0, & \text{otherwise} \end{array} \right. \end{equation}
Thus U(x) ≡ 1 and ∅(x) ≡ 0. The complement of primitive object Oi can be defined by function: $$O_i^c(x)= 1-O_i(x)$$ the intersection of k objects: $$\min_{i = 1 \dots k}(O_i(x))$$ the union of k objects: $$ \max_{i = 1 \dots k}(O_i(x))$$ the difference of two objects: $$\min\left(O_i(x), 1-O_j(x)\right)$$
With the binary connection matrices WC , WI and WU , each node in the CSG-Stump structure can be defined by a certain function.
For each node i = 1,···,K in the first layer, its shape Fi can be defined by function Fi(x):
\begin{equation}\label{eq:Fi} F_i(x) = W_C[1,i]\times (1-O_i(x)) + (1-W_C[1,i])O_i(x). \end{equation}
For each node i = 1,···,C in the second layer, its shape Si is an intersection of nodes from the first layer, and can thus be defined by function Si(x):
\begin{equation} \label{eq:Si} S_i(x) = \min_{1 \le j\le K}(W_{I}[j,i] \times F_j(x) + (1-W_{I}[j,i]) \times 1). \end{equation}
For the node in the third layer, its shape T is the union of nodes from the second layer, and can thus be defined by function T (x):
\begin{equation}\label{eq:Tx} T(x) = \max_{1\le j\le C}(W_{U}[j,1] \times S_j(x) + (1-W_{U}[j,1]) \times 0). \end{equation}
Now for a input shape given by a point cloud X = {xi}N consisting of a list of 3D points xi, we can first obtain the target shape occupancy Oi as aboved occupancy function O(x) and then detect the underlying primitives with a RANSAC-like method. Then reconstructing a CSG-like representation for the shape is simplified to finding the three connection matrices which can be formulated as a Binary Programming problem.
let Ok(i) represents the occupancy value of testing point i for primitive k and T(i) represents the estimated occupancy of point i. The connection matrices WC,WI and WU for the selection process of CSG-Stump are the solution of the following minimization problem:
$$ \small \begin{align} \underset{W_{\{C,I,U\}}}{\text{min.}}& \quad \frac{1}{N}\sum_i^N{\|T(i)-O_i\|}\nonumber\\ \textrm{s.t.}\quad &T(i)=\max_j\{S_j(i) \times W_{U}[j,1] \} \nonumber\\ &S_j(i)=\min_k\{F_{k}(i) \times W_{I}[k,j]+(1-W_I[k,j])\} \nonumber\\ &F_k(i)=(1-O_{k}(i)) W_{C}[1,k] + {O}_{k}(i) (1-W_{C}[1,k]) \nonumber\\ &W_{I}, W_{U}, W_{C}\in\{0,1\},\;\; {O}_{k}(i)\in\{0,1\} \end{align} \normalsize $$
We prove that CSG-Stump is equivalent to typical CSG-Tree in terms of representation, i.e., we can represent anycomplex CSG shape by our three-layer CSG-Stump. Therefore, CSG-Stump inherits the ideal characteristics of CSG-Tree, allowing highly compact, interpretable and editable shape representation while freeing from the limitations of a tree structure. Moreover, CSG-Stump gives rise to two additional advantages: 1) High representation capability. The maximum representation capability can be realistically achieved with CSG-Stump, as opposed to a conventional CSG-Tree that needs many layers for complex shapes. 2) Deep learning-friendly. The consistent structure of CSG-Stump allows neural networks to give fixed dimension output, making network design much easier.
CSG-Stump Net
When a relatively large number of primitives are required to represent a shape, Binary Programming typically fails to obtain an optimal solution in polynomial time due to the combinational nature of the problem. We therefore propose a learning-based approach by designing CSG-StumpNet to jointly detect primitives and estimate CSG-Stump connections. As illustrated in the right figure, CSG-Stump Net first encodes a point cloud into a latent feature and then decodes it via the primitive head and the connection head respectively. Primitive head decodes latent features into a set of K parametric primitives where each parametric primitive is represented by intrinsic and extrinsic parameters. Connection head decodes the encoded features into the connection matrices WC , WI and WU. Then we obatin occupancy by occupancy calculator which computes the primitive’s Signed Distance Field (SDF) first and then converts it to occupancy through sigmoid function Φ: \begin{equation} \label{eq:ox} O(x)=\Phi(-\eta \times SDF(x)), \end{equation} Given the predicted primitives occupancy and connection matrices, we finally calculate the occupancy of the overall shape using CSG-Stump Constructor. We directly employ an off-the-shelf backbone, i.e. DGCNN, as the encoder. Note that our framework is fully compatible with other backbones as well.
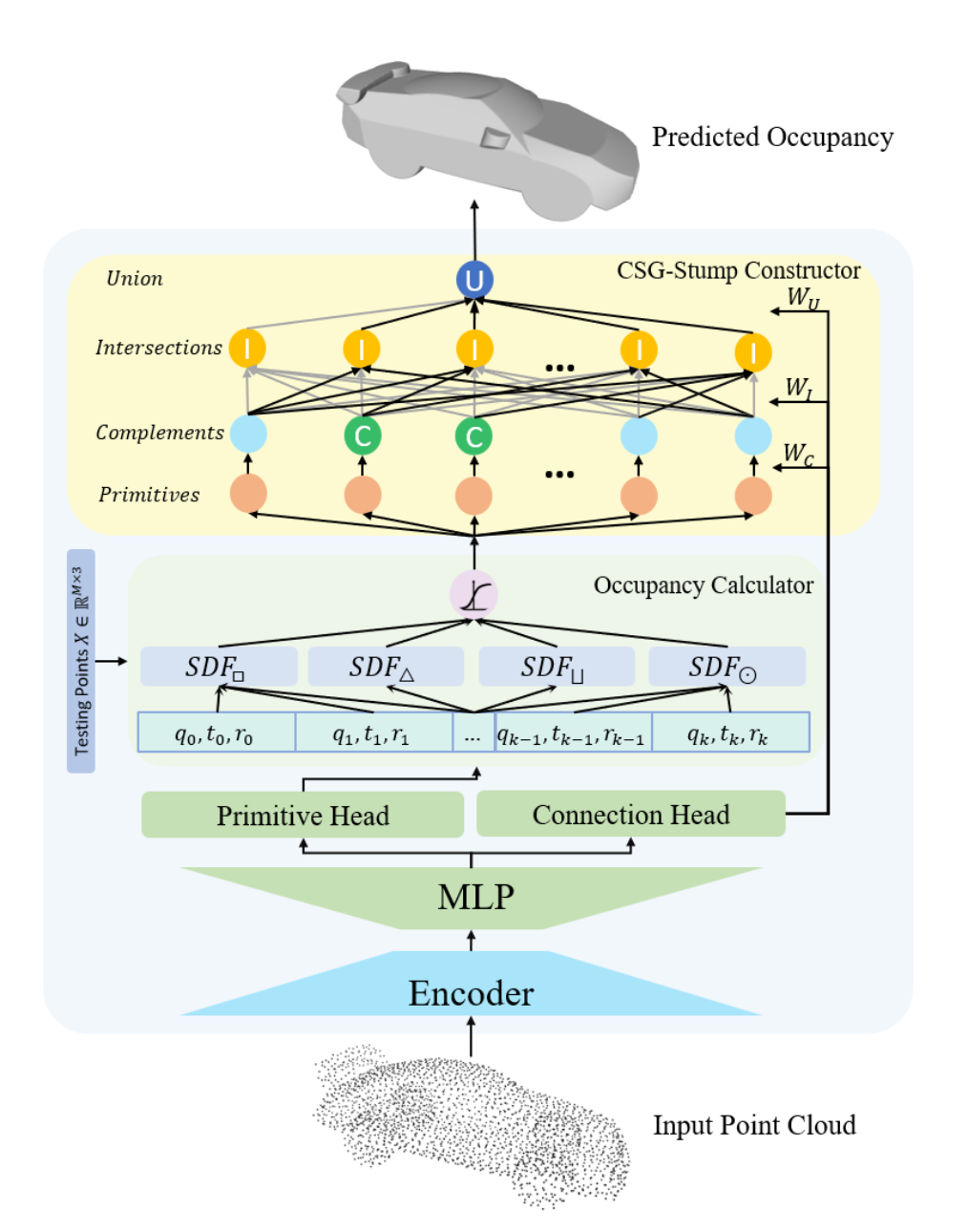
Training
We train CSG-Stump Net end-to-end in an unsupervised manner, without explicit ground truth. Instead, the supervision signal is quantified by the reconstruction loss between the predicted and ground truth occupancy as follows: \begin{equation} L_{recon} = \mathbb{E}_{x\sim X}||\hat{O}_i-O^*_i||_2^2. \end{equation}
We also propose a primitive loss to pull each primitive surface to its closest test point, which prevents the gradient from vanishing. We define this loss term as \begin{equation} L_{primitive} = \frac{1}{K}\sum_k^K \min_{n}SDF_{k}^2(x_n), \end{equation} where SDFk(xn) computes the SDF of test point xn to primitive k.
Finally, the overall objective can be defined as the joint loss of the above two terms: \begin{equation} L_{total} = L_{recon} + \lambda \cdot L_{primitive}, \end{equation} where the balance term λ is set to 0.001 empirically.
We also propose a primitive loss to pull each primitive surface to its closest test point, which prevents the gradient from vanishing. We define this loss term as \begin{equation} L_{primitive} = \frac{1}{K}\sum_k^K \min_{n}SDF_{k}^2(x_n), \end{equation} where SDFk(xn) computes the SDF of test point xn to primitive k.
Finally, the overall objective can be defined as the joint loss of the above two terms: \begin{equation} L_{total} = L_{recon} + \lambda \cdot L_{primitive}, \end{equation} where the balance term λ is set to 0.001 empirically.
Evaluate CSG-Stump Net
Comparison on Statistic Evaluation Results
We evaluate results on the L2 Chamfer Distance between 2048 sampled points on a reconstructed shape and those on the corresponding ground truth following UCSG-Net. The quantitative results are reported in the following table. Note that results of VP, SQ and UCSGNet are using reported results in UCSG-Net. We can see that CSG-Stump Net outperforms both kinds of methods and improve previous SOTA results by over 9%.


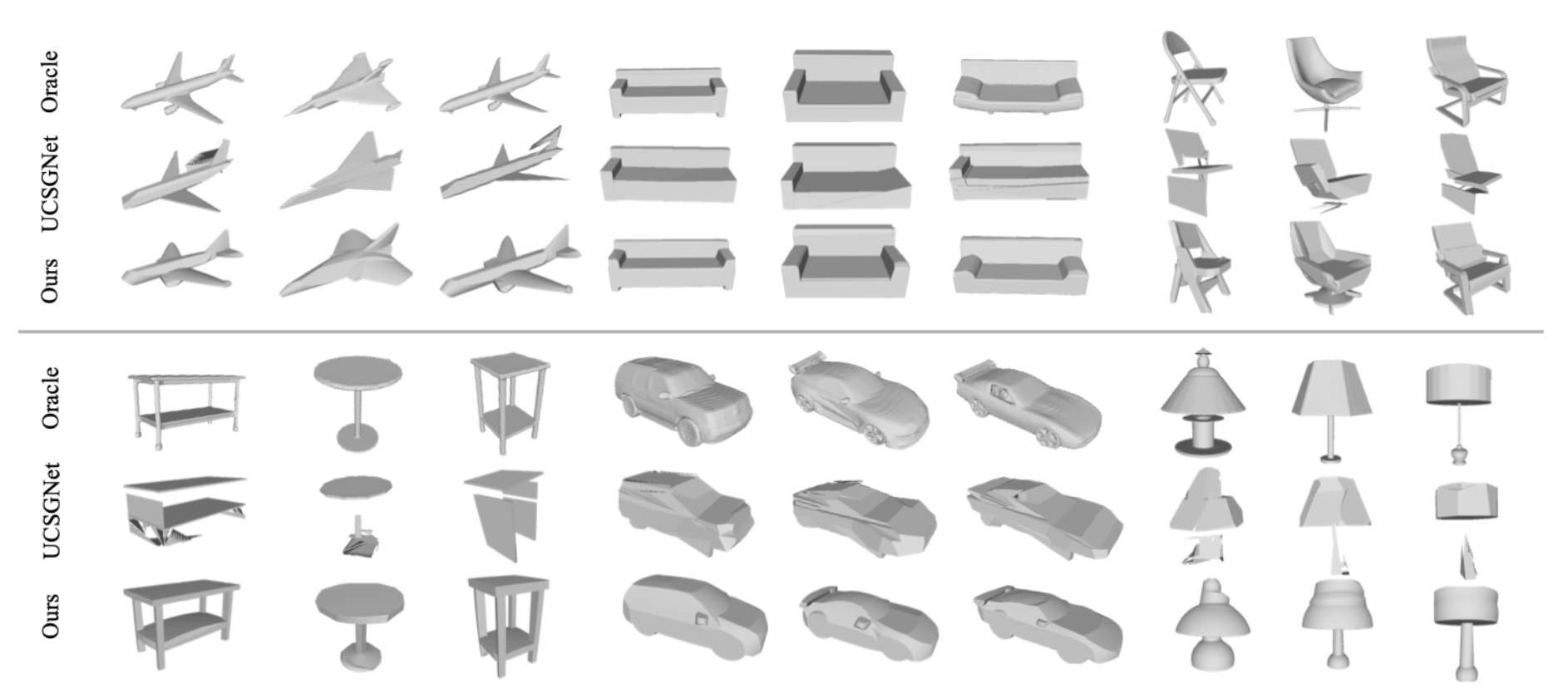
Comparison on Geometric Evaluation Results
The following figure shows the qualitative comparison with the CSG-like counterpart, i.e. UCSG-Net We can see our method achieves much better geometry approximation and structure decomposition in comparison to oracle shapes.

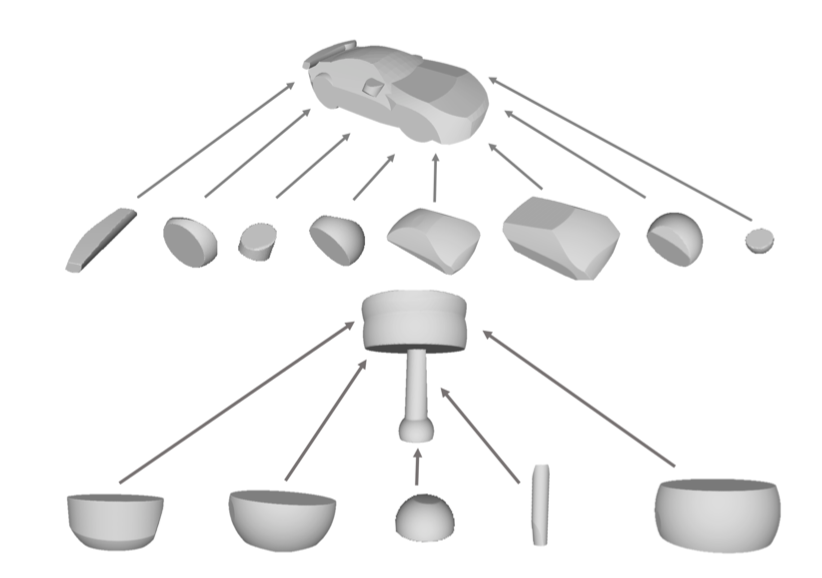
Performance on Compactness
The right figure shows the generated CSG-stump structures of the car and lamp examples. We can see that only a small subset of intersection nodes are used to construct the final shape, which suggests the obtained structure is compact. Interestingly, the automatically learned intersection nodes are consistent to semantic part decomposition of car and lamp, which may be useful for other tasks such as part segmentation.
Performance on Editability
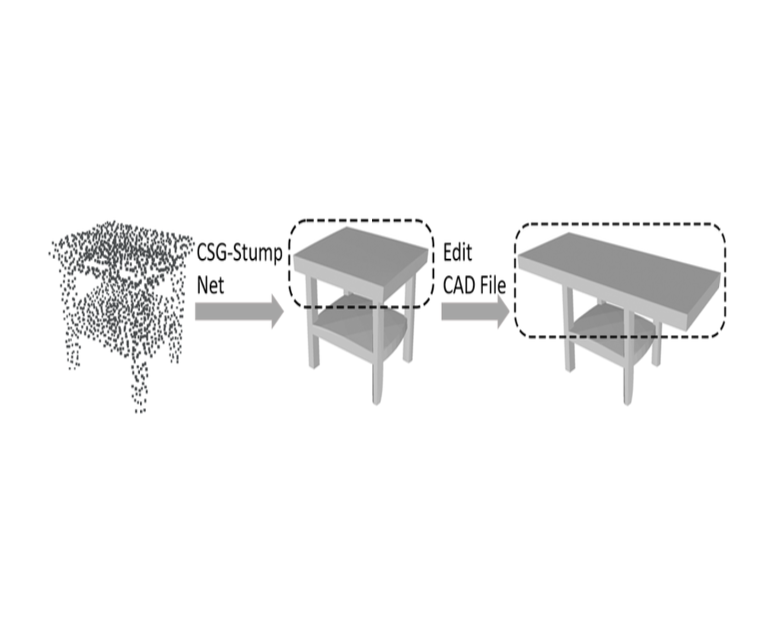
As CSG-Stump is equivalent to CSG, we are allowed to edit primitives and CSG-Stump connections for further designs. Specifically, we implemented a simple adaptor to convert our outputs to the input format of OpenSCAD files, where OpenSCAD is an open-sourced CAD software. By leveraging OpenSCAD’s editing user interface and CSG-Stump Net, a user can achieve a design aim directly based on a point cloud.
Acknowledgement
The work is partially supported by a joint WASP/NTU project (04INS000440C130)